地球重达60万亿亿吨，为何能悬在空中，没有掉下去呢？

英国诗人亚历山大·蒲柏曾说：自然和自然的法则在黑夜中隐藏；上帝说，让牛顿去吧！于是一切都被照亮。

获得这句赞誉的原因之一，是牛顿敏锐地洞察到了宇宙中任何具有质量的物体都会相互吸引。他把这称为universal gravitation——万有引力。并用数学方法求证出了两个物体间的引力大小，与物体质量的乘积成正比，与它们距离的平方成反比。

这一伟大的发现让人类知道了，地球上悬空的苹果、石块、铁球等物体之所以会“向下掉落”，是由于它们受到了地球引力的牵引，从而纷纷呈现出了朝地心方向运动的趋势。我们通常所理解的“重量”，其实就是物体的质量在地球引力环境下的外在表现。我们直观感受到有重量的物体会“向下掉落”，也不过是由于站在地球的任意位置，地心都在我们的“脚下”而已。

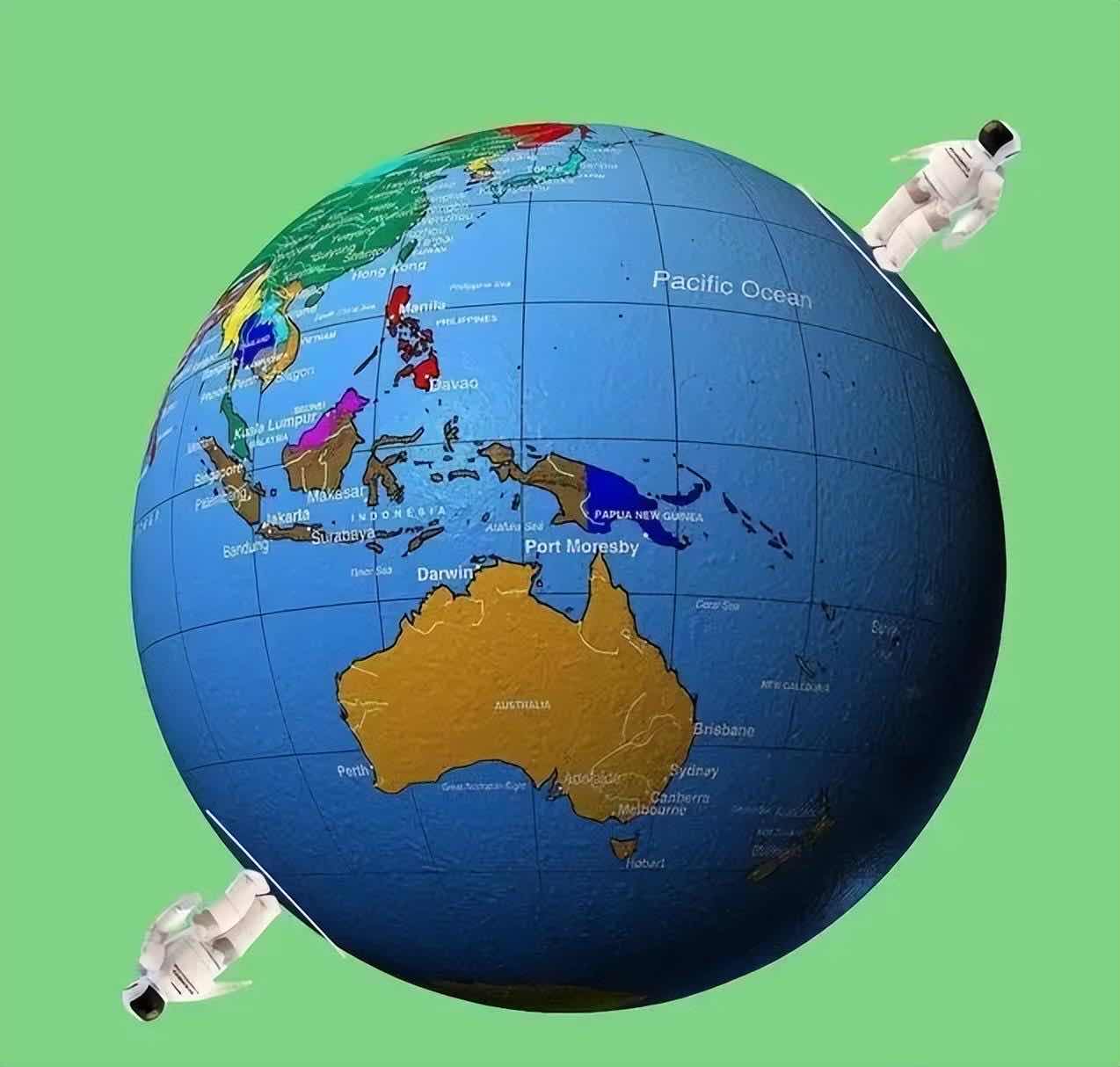
换句话来说，下方本身就是一个相对的概念，如果把视野扩大，从宇宙的视角观看就会清晰地发现，北极和南极的下方是两个截然相反的方向。

由此我们也就不难想到，宇宙中其实并没有一个固定的“下方”，甚至可以说根本就没有“下方”这个概念，假如地球要朝某个方向“掉落”，则必然是受到了某个引力的牵引，而不会是“向下”掉落。

在知识普及程度极高的今天，想必所有人都早已知道了地球与太阳系中的所有天体之间都存在引力，而其中强度最大的引力来自于太阳，这便是地球围绕着太阳公转的原因。与此同时，这也就意味着，地球如果要掉入某个地方，那就只能是掉入太阳了。

所以地球为什么没有坠入太阳呢？

关于这个问题，许多人都认为是地球的惯性抵消了太阳的引力，但这样理解很不严谨，事实上惯性并不能抵消引力，物体在作惯性运动的时候仍然无时不刻地被引力影响着。

惯性是一个虚拟的作用力，它会使地球具有朝某个固定的方向做匀速直线运动的趋势，而太阳的引力则会使地球产生朝太阳的中心做直线运动的趋势，这两种力始终共同作用于地球，致使地球无法沿着任何方向做直线运动，只能沿着一条弧线做曲线运动了。

牛顿曾用一个十分聪慧的思想实验清晰地诠释过这个问题。

首先我们需要忽略掉地面的所有山峰以及空气，把地球想象成一个没有空气阻力影响的完全光滑的圆球。其次还需要说明一下，在地球表面的重力加速度下，初始速度为0，且作自由落体运动的物体，在第1秒大约会掉落4.9米（s=0.5gt^2,g=9.8,t=1,则s=4.9米）。

现在，假设我们在4.9米高的位置松手放开一颗铁球，它毋庸置疑会沿着一条垂直于地面的轨迹落在我们脚下，耗时为1秒。

可如果我们不是松手放开，而是以每秒10米的初速将这颗铁球朝平行于地面的方向发射出去，铁球就会沿着一条弧线掉落到距离我们10米远的地方，耗时同样是1秒。

这是由于铁球此时同时具有了两个方向的运动速度——水平方向的惯性速度使它向前运动了10米，垂直方向的速度则使它向下运动了4.9米，所以它会刚好掉落在10米远的地方，这在物理学中被称为“平抛运动”。

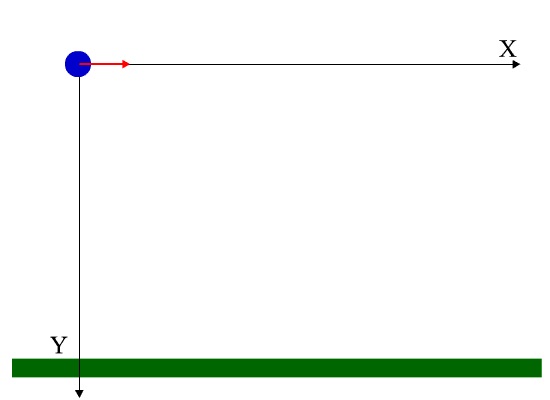
按照这个规律继续推断，我们便能得知，如果铁球的发射初速为每秒50米，它会在1秒内向前运动50米，向下运动4.9米，最后掉落到50米远的地方；初速为100米，1秒后则会掉落在100米远的地方。也就是说，无论铁球的惯性速度是多少，它始终会在引力的作用下每秒向下运动4.9米。显而易见，惯性速度丝毫也没有抵消引力对它造成的影响。

那么问题来了：假如铁球的惯性速度为每秒7900米，结果会如何呢？

毋庸置疑的是，即便速度为每秒7900米也不会抵消引力的影响，这颗铁球仍然会每秒向下运动4.9米，因此1秒后它就会掉落在距离我们7900米远的地方，对么？

遗憾的是，答案是否定的。

事实上，当铁球的惯性速度为7900米时，它虽然还是会每秒向下运动4.9米，然而却再也无法掉回地面了，而是永远保持距离地面4.9米的高度，绕着地球不停地转圈圈。

这乍一听似乎有点矛盾，怎么会又在向下掉落，又永远保持相同的高度呢？

其实答案很简单，因为地球是圆的！

地面本身就是一直“向下弯曲”的，当铁球的惯性速度为7900米时，它的运动轨迹正好与地面的弯曲幅度相吻合。当铁球向下运动4.9米时，地面也恰好“向下”弯曲了4.9米，于是铁球就始终无法接触到地面，只能在不断“坠落”的同时，永远停留在4.9米的高度了。

下面的动图能一目了然地看见这个现象。

上图中的铁球惯性速度为每秒7000米，这个速度能让它在一个距离起点十分遥远的地方掉回地面。

下图中的铁球惯性速度则为每秒7900米，这个速度会让它沿着一条十分理想的圆形轨道环绕地球运动。

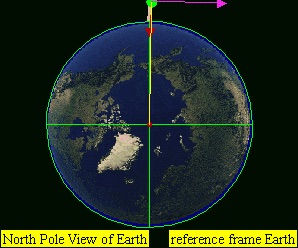
正因如此，7900米/秒通常被称为“环绕速度”，也叫第一宇宙速度，任何物体一旦达到这个速度，就能在近地轨道上环绕地球运动。

但需要说明一下，在不同的高度上，物体环绕地球的速度其实是有所差异的，因为不同高度的引力强度不同。例如月球的平均公转速度仅有1.023千米/秒，远低于第一宇宙速度，但由于它距离地心很远，受到的引力强度也远低于近地轨道上的人造飞行器，所以它仍然会始终环绕地球运行。

此外，沿着如此理想的圆形轨道公转需要极其理想的速度才能实现，一般来说只有人造飞行器才能做到，自然天体的惯性速度是不会如此理想的。

速度不够理想时会出现什么情况呢？

假如近地轨道上的某个飞行器的速度大于第一宇宙速度（环绕速度），小于第二宇宙速度（逃逸速度），它便会沿着一条椭圆形的轨道环绕地球运行，如下图所示。

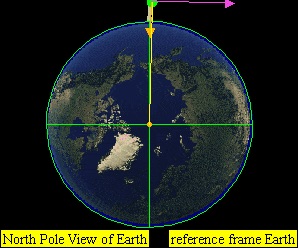
这颗铁球的初速为8000米/秒，这个速度是大于环绕速度的，这会导致它具有远离地球的趋势，然而，在它远离地球的过程中，会由于引力的拉扯而不断减速，最终又因为速度太慢被拉回地球。而在接近地球的过程中，它又开始不断加速，最终回到8000米/秒的初速，于是又开始远离地球……就这样，它开始周而复始地沿着椭圆轨道运行了。

换言之，即使某个物体的惯性速度大于环绕速度，它也不见得能逃离地球，除非它的速度已经达到了第二宇宙速度，才能摆脱地球的控制，这个速度在近地轨道的高度约为10.9公里/秒。

这便是天体围绕另一个天体公转的本质原因，从这个意义上来说，地球其实一直就在惯性和引力的共同作用下，沿着一条弧线坠向太阳，只不过地球的公转速度使它坠落的曲线正好跟太阳表面的弯曲幅度相接近，以至于始终在同一个椭圆形的轨道上转圈圈，无法与太阳发生实际接触而已。