戴维南定理实验报告结论(戴维南定理实验报告数据分析及实验结论)
戴维南定理实验报告结论(戴维南定理实验报告数据分析及实验结论)
根据实验结果,我们可以得出戴维南定理的结论:在一个电路中,当电阻、电流、电势差任意两个量已知时,第三个量可以通过戴维南定理来计算得出。戴维南定理是电学中十分重要的定理之一,可以帮助我们更好地理解电路中的各种关系,并且在实际应用中也有广泛的应用。
关于电路分析实验报告
戴维南定理及功率传输最大条件
一、实验目的
1、用实验 *** 验证戴维南定理的正确性。
2、学习线性含源一端口网络等效电路参数的测量 *** 。
3、验证功率传输最大条件。
二、原理及说明
1、戴维南定理
任何一个线性含源一端口网络,对外部电路而言,总可以用一个理想电压源和电阻相串联的有源支路来代替,如图3-1所示。理想电压源的电压等于原网络端口的开路电压UOC,其电阻等于原网络中所有独立电源为零时入端等效电阻R0 。
2、等效电阻R0
对于已知的线性含源一端口网络,其入端等效电阻R0可以从原网络计算得出,也可以通过实验手段测出。下面介绍几种测量 *** 。
*** 1:由戴维南定理和诺顿定理可知:
因此,只要测出含源一端口网络的开路电压UOC和短路电流ISC, R0就可得出,这种 *** 最简便。但是,对于不允许将外部电路直接短路的网络(例如有可能因短路电流过大而损坏网络内部的器件时),不能采用此法。
*** 2:测出含源一端口网络的开路电压UOC以后,在端口处接一负载电阻RL,然后再测出负载电阻的端电压URL ,因为:
则入端等效电阻为:
*** 3:令有源一端口网络中的所有独立电源置零,然后在端口处加一给定电压U,测得流入端口的电流I (如图3-2a所示),则:
也可以在端口处接入电流源I′,测得端口电压U′(如图3-2b所示),则:
3、功率传输最大条件
一个含有内阻ro的电源给RL供电,其功率为:
为求得RL从电源中获得最大功率的最佳值,我们可以将功率P对RL求导,并令其导数等于零:
解得:RL=r0
得最大功率:
即:负载电阻RL从电源中获得最大功率条件是负载电阻RL等于电源内阻r0 。
三、仪器设备
电工实验装置 :DG011 、 DY031 、 DG053
四、实验内容
1、线性含源一端口网络的外特性
按图3-3接线,改变电阻RL值,测量对应的电流和电压值,数据填在表3-1内。根据测量结果,求出对应于戴维南等效参数Uoc,Isc。
表3-1线性含源一端口网络的外特性
RL(Ω) 0短路 100 200 300 500 700 800 ∞开路
I(mA)
U( V )
2、求等效电阻Ro
利用原理及说明2中介绍的3种 *** 求R。,并将结果填入表3-2中, *** (1)和 *** (2)数据在表3-1中取, *** (3)实验线路如图3-4所示。
表3-2等效电阻R0
*** 1 2 3
R0(KΩ)
R0的平均值
3、戴维南等效电路
利用图3-4构成戴维南等效电路如图3-5所示,其中U0=R0=。
测量其外特性U=f(I)。将数据填在表3-3中。
表3-3戴维南等效电路
RL(Ω) 0短路 100 200 300 500 700 800 ∞开路
I(mA)
U( V )
4、最大功率传输条件
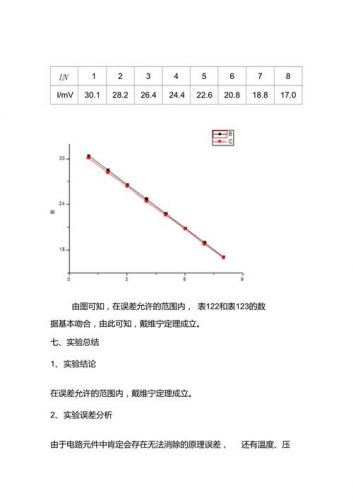
1.根据表3-3中数据计算并绘制功率随RL变化的曲线:P=f(RL) 。
2.观察P=f(RL)曲线,验证最大功率传输条件是否正确。
六、报告要求
1、 根据实验1和3测量结果,在同一张座标纸上做它们的外特性曲线U=f(I),并分析比较。
2、 完成实验内容2的要求。
戴维南定理及功率传输最大条件
一、实验目的
1、用实验 *** 验证戴维南定理的正确性。
2、学习线性含源一端口网络等效电路参数的测量 *** 。
3、验证功率传输最大条件。
戴维南定理实验结果?
是成立的。
因为戴维南定理是在直角三角形中成立的,而直角三角形是非常基础的几何概念,在实验中可以通过多组数据验证该定理的正确性。
此外,戴维南定理在实际生活中的应用也非常广泛,比如在建筑、测量等领域都能够得到应用,因此学习和掌握该定理是非常重要的。
戴维南定理不仅适用于直角三角形,也适用于任意一个三角形。
对于任意一个三角形ABC,设它的三边分别为a、b、c,其内角A、B、C所对的边分别为a、b、c,则有:a^2=(b+c)(b+c-a)/4b^2=(a+c)(a+c-b)/4c^2=(a+b)(a+b-c)/4该定理可以用于解决对角线长度、平行线距离、垂足的计算问题。
戴维南定理又称为两杆定理,是关于刚体静力学的一个基本定理。该定理表明:在一定条件下,一个刚体在静止的情况下,受力平衡时,其受力点处的合力为零,且其受力点处的力矩也为零。
戴维南定理已经在实验中得到了验证。例如,在一个悬挂木块的实验中,通过多个张力传感器测量力的大小和方向,可以得到这些力的合力为零,验证了戴维南定理。此外,在许多基础力学实验中也都得到了戴维南定理的验证。
已被证实因为经过多次实验验证,戴维南定理已经被证实。
戴维南定理是在数学中关于多项式解的一个重要定理,其定理表明任何一个数域上的n元多项式方程,都至少有一个解在该数域上。
这个定理在代数学和数论中有着广泛的应用。
戴维南定理还有它的推论——伊文诺定理,即一个n元不可约多项式f(x1,x2,…,xn),与所有由该多项式通过有限次加、减、乘、除及可以求解的根式运算得到的多项式最大公因式g(x1,x2,…,xn)相等。
戴维南定理在数学中有着重要的地位,它不仅仅是解决多项式问题的重要工具,还有着广泛的拓展用途。