​数学史三大危机简介（数学史上的三次数学危机）

数学史三大危机简介（数学史上的三次数学危机）

数学这一门学科发展到现在，有了许许多多的分支，也与其他学科发生着千丝万缕的联系。那么，数学史上的三次危机，你知道吗？

第一次数学危机

第一次数学危机发生于公元前400年的古希腊。这次危机自根号二的发现起，到公元前370年左右，直到无理数的定义出现才宣告结束。

众所周知，古希腊有一位大哥级的数学家——毕达哥拉斯（记住了，不是毕达哥斯拉），他创立了一个学派——毕达哥拉斯学派。这个学派认为“万物皆数”，他们要接受长期的训练和考核，遵守很多的规范和戒律，并且宣誓永不泄露学派的秘密和学说。他们相信依靠数学可使灵魂升华，与上帝融为一体，万物都包含数，甚至万物都是数，上帝通过数来统治宇宙。

毕达哥拉斯

相传，毕达哥拉斯应邀参加一次豪华聚会，不知道什么原因，大餐迟迟不上桌。善于观察和理解的毕达哥拉斯没有注意这些，而是被脚下规则、美丽的方形石砖所深深吸引，他不是在欣赏它们的美丽而是在思考它们和“数”之间的关系。于是，在大庭广众之下，他蹲在地板上，拿了画笔在选定的一块石砖上以它的对角线为边画一个正方形，结果惊奇的的发现这个正方形的面积恰好等于两块砖的面积和。开始他以为这只是巧合，但当他把两块砖拼成的矩形之对角线做另一个正方形时，这个正方形面积相当于5块砖的面积。这也就是说它等于以两股为边作正方形面积之和。后来，他又做了进一步演算，最终证明了“毕达哥拉斯定理”（即勾股定理）。

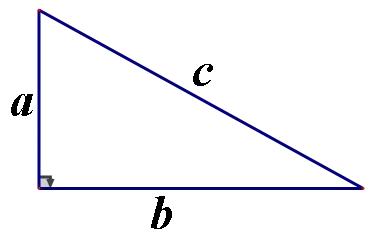
a² b²=c²

毕达哥拉斯认为数字分三类，一类是整数，一类是有限小数，还有一类是无限循环小数。这些数字都有一个共同点，那就是他们都可以用整数之比来表示，这些数被称为“有理数”，而毕达哥拉斯所认为的“万物皆数”，就是指所有实数都是有理数。毕达哥拉斯在当时的影响力是相当大的，因而几乎所有人都毫无疑义地认同了这种说法。

这时，一位名叫希帕索斯的小哥出场了，他发现以下直角三角形的斜边不能用整数之比来表示：

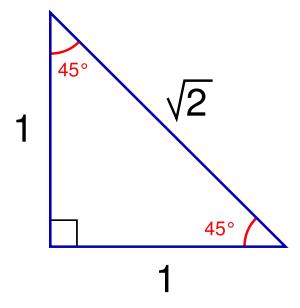
据说，毕达哥拉斯在听到这个说法后十分震惊，要求所有成员不得泄露这个数的存在，甚至杀害了可怜的小哥希帕索斯。这是数学史上第一次发现无理数。（P.S.也有说法称正五边形的边长与对角线长是最先被发现的无理数）

第一次数学危机是由无理数的发现引起的，只要准确的给无理数下一个定义就可以漂亮地解决这个问题。那就有人要问了，无理数的定义到底怎么下呢?这对当时的人来说是一个问题。

这个问题是在约公元前370年，由柏拉图的学生攸多克萨斯解决的。他用公理化方法创立了新的比例理论，巧妙地处理了可公度和不可公度。他处理不可公度的办法，被欧几里得《几何原本》第二卷（比例论）收录。

值得一提的是，攸多克萨斯给出的解释与狄德金于1872年给出的无理数的现代解释几乎完全一致。

至此，第一次数学危机得到解决，这是一次数学史上的革命，产生了深远的影响。它使得古希腊传统的数学思想得到冲击，整数的地位也受到了挑战，几何学开始蓬勃发展。也正是因为这一次数学危机，数系得到了扩充，人们开始接受无理数的存在。

,