爱情函数-心形线
爱情函数-心形线
2019年高考数学命题以立德树人为根本,全面考查了德智体美劳几个方面,尤其是美育和劳动教育。数学的美体现在简洁、对称、周期、和谐。
参考例题: 理科8题关注了著名的“心形”曲线,形状优美、寓意美好,使学生得到了美的熏陶。

分析:


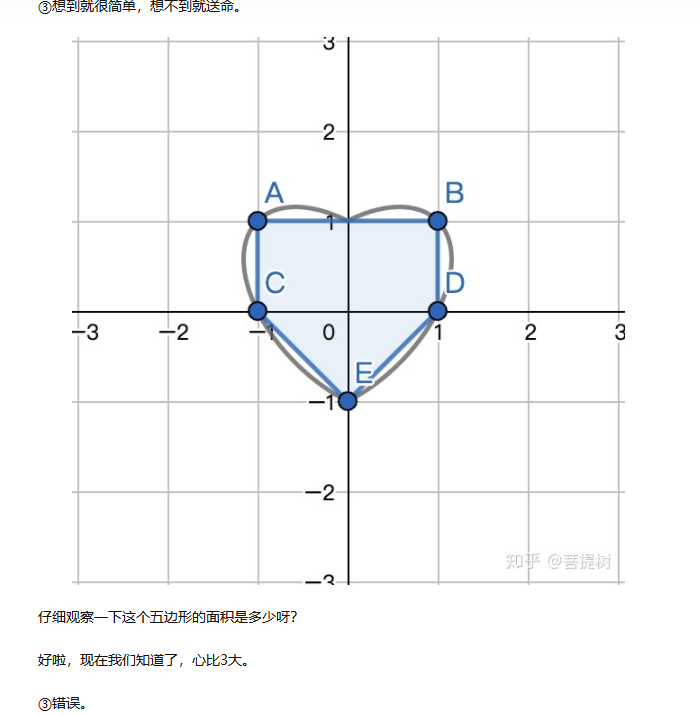
所以正确选项是C。
背景故事
1650年,在斯德哥尔摩的街头,52岁的大数学家笛卡尔,身上只有衣服和几本数学书。性格高傲的他,从不向路人乞求,只是在低头写写画画,沉醉于他自己的数学世界。
一个宁静的午后,笛卡尔照例坐在街头研究他的数学,突然有人从背后拍他的肩膀,也就在这个时候,他邂逅了18岁的克里斯汀公主。两人长达三小时的交谈,笛卡尔发现公主对数学的浓厚兴趣,彼时的他还不知道身边这位女孩的身份;没过多久,他就被聘用为了公主的御用数学老师。
公主在笛卡尔的悉心指导下突飞猛进,然而每天的形影不离,也让这对爷孙产生了爱慕之心。于是,美好的爱情种子悄然发芽,而且以迅雷不及掩耳之势从小树苗成为了大树。
后来的结果可想而知,笛卡尔被放逐,公主则被软禁。离开公主的笛卡尔,坚持写信给公主,表达思念之苦。然而都被国王拦了下来,而他自己带着遗憾,永远的离开了人世。这边的克里斯汀公主,绝食抵抗,一天天消瘦下来,国王不忍心,于是将笛卡尔的最后一封信交给了她。
拿到信的公主,用笔和纸画出的信上的那个方程(r=a(1-sinθ)),一个爱心,也就是著名的心形线。公主潸然泪下,后来公主继承王位,寻找笛卡尔,却只听到去世的消息。而这分享誉世界的情书,至今还保存在欧洲迪卡尔的纪念馆里。

扩展资料:
心形线,是一个圆上的固定一点在它绕着与其相切且半径相同的另外一个圆周滚动时所形成的轨迹,因其形状像心形而得名。
心脏线亦为蚶线的一种。在曼德博集合正中间的图形便是一个心脏线。心脏线的英文名称“Cardioid”是 de Castillon 在1741年的《Philosophical Transactions of the Royal Society》发表的;意为“像心脏的”。
1、极坐标方程
水平方向: ρ=a(1-cosθ) 或 ρ=a(1+cosθ) (a>0)
垂直方向: ρ=a(1-sinθ) 或 ρ=a(1+sinθ) (a>0)
2、直角坐标方程
心形线的平面直角坐标系方程表达式分别为 x^2+y^2+a*x=a*sqrt(x^2+y^2) 和 x^2+y^2-a*x=a*sqrt(x^2+y^2)
3、参数方程
-pi<=t<=pi 或 0<=t<=2*pi
x=a*(2*cos(t)-cos(2*t))
y=a*(2*sin(t)-sin(2*t))
所围面积为3/2*PI*a^2,形成的弧长为8a
所围面积的求法:以ρ=a(1+cosθ)为例
令面积元为dA,则
dA=1/2*a∧2*(1+cosθ)∧2*dθ
运用积分法上半轴的面积得
A=∫(π→0)1/2*a∧2*(1+cosθ)∧2*dθ=3/4*a∧2*π
所以整个心形线所围成的面积S=2A=3/2*a∧2*π
笛卡尔的心形攻势的内容就是好以上的内容,可能高中的同学比较难看懂的,基本上进入大学之后学习了高等数学可能就相对比较明白了!